Title: Efficient simulation of ultrafast quantum nonlinear optics with matrix product states [Optica, arXiv, PDF]

Authors: Ryotatsu Yanagimoto, Edwin Ng, Logan G. Wright, Tatsuhiro Onodera, and Hideo Mabuchi

Published on 5 October 2021.

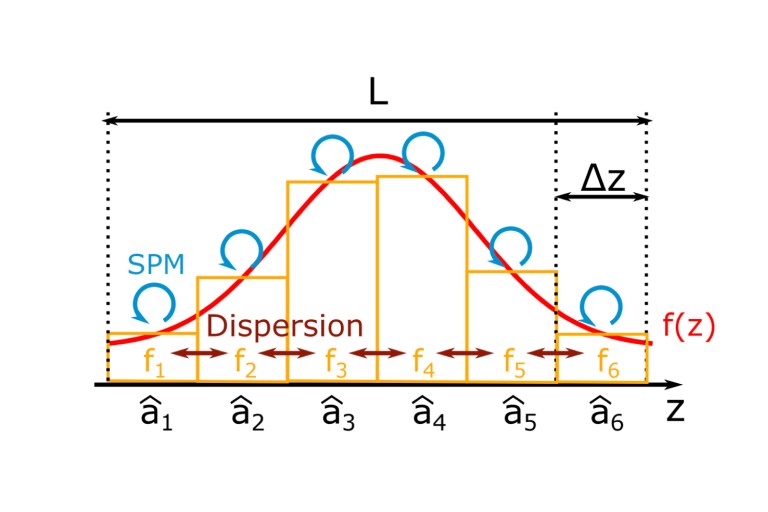
Abstract: Ultra-short pulses propagating in nonlinear nanophotonic waveguides can simultaneously leverage both temporal and spatial field confinement, promising a route towards single-photon nonlinearities in an all-photonic platform. In this multimode quantum regime, however, faithful numerical simulations of pulse dynamics naïvely require a representation of the state in an exponentially large Hilbert space. Here, we employ a time-domain, matrix product state (MPS) representation to enable efficient simulations by exploiting the entanglement structure of the system. In order to extract physical insight from these simulations, we develop an algorithm to unravel the MPS quantum state into constituent temporal supermodes, enabling, e.g., access to the phase-space portraits of arbitrary pulse waveforms. As a demonstration, we perform exact numerical simulations of a Kerr soliton in the quantum regime. We observe the development of non-classical Wigner-function negativity in the solitonic mode as well as quantum corrections to the semiclassical dynamics of the pulse. A similar analysis of χ(2) simultons reveals a unique entanglement structure between the fundamental and second harmonic. Our approach is also readily compatible with quantum trajectory theory, allowing full quantum treatment of propagation loss and decoherence. We expect this work to establish the MPS technique as part of a unified engineering framework for the emerging field of broadband quantum photonics.